How We Find and Characterize

Since the first confirmation of an exoplanet orbiting a Sun-like star in 1995, and with only a small sampling of our Milky Way galaxy so far surveyed, we’ve already struck many rich veins.

A statistical estimate based on data from NASA’s Kepler Space Telescope revealed that there are more planets than stars in our galaxy. That means there are more than a trillion planets in our galaxy alone, many of them in Earth’s size range.

“Right now we know, for the first time, that small planets are very common,” said Sara Seager, a professor at the Massachusetts Institute of Technology and an exoplanet research pioneer. “It’s phenomenal. We had no way to know that before Kepler. We’ll just say, colloquially: They’re everywhere.”

artist's concept of an exoplanet surface

This artist's conception shows a young, hypothetical planet around a cool star. A soupy mix of potentially life-forming chemicals can be seen pooling around the base of the jagged rocks. Observations from NASA's Spitzer Space Telescope hint that planets around cool stars – the so-called M-dwarfs and brown dwarfs that are widespread throughout our galaxy – might possess a different mix of life-forming, or prebiotic, chemicals than our young Earth.

NASA/JPL-Caltech/T. Pyle

The planet discovered in 1995 was a hot, star-hugging gas giant believed to be about half the size of Jupiter. It tugged so hard on its parent star as it raced around in a four-day orbit that the star’s wobbling was obvious to earthly telescopes – once astronomers knew what to look for.

Artist's concept of 51 Pegasi b, also called "Dimidium," was the first exoplanet discovered orbiting a star like our Sun. This groundbreaking find in 1995 confirmed planets like Earth could exist elsewhere in the universe.

NASA

Finding this fast-moving gas giant, known as 51 Pegasi b, kicked off what might be called the “classical” period of planet hunting. The early technique of tracking wobbling stars revealed one planet after another, many of them large “hot Jupiters” with tight, blistering orbits.

The wobble method measures changes in a star’s “radial velocity.” The wavelengths of starlight are alternately squeezed and stretched as a star moves slightly closer, then slightly farther away from us. Those gyrations are caused by gravitational tugs, this way and that, from orbiting planets.

The Kepler Space Telescope (2009-2018) ushered in what we could call the “modern” era of planet hunting. Kepler settled into an Earth-trailing orbit, then fixed its gaze on a small patch of sky. It stared at that patch for four years.

Within that small patch were 150,000 stars. Kepler was waiting to catch tiny dips in the amount of light coming from individual stars, caused by planets crossing in front of them. This is called “transit method.” Once detected, the planet's orbital size can be calculated from the period (how long it takes the planet to circle once around the star) and the mass of the star.

NASA’s Transiting Exoplanet Survey Satellite, launched in 2018, employs the same technique (it’s in the name, afterall) to survey whole swaths of our sky. Space telescopes like Spitzer and Hubble have been used to discover exoplanets and reveal more information about what they’re like. From mass characterizations to elements in atmospheres to planetary weather maps.

Our eyes in space will grow sharper, begin to scrutinize the atmospheres of extremely distant planets, and even capture direct images of some of these worlds – perhaps another small, rocky, blue and white marble.

Once light is captured, it can be probed to reveal the composition of exoplanet atmospheres. Think of a prism: shine white light through it, and it splits the light into a rainbow spectrum. Scientists can read the color bands of this spectrum like a bar code, revealing which molecules are present.

NASA’s James Webb Space Telescope has several powerful scientific instruments, called spectrographs, on board. With these, scientists can look at newly forming planetary systems and identify the unique signatures of molecules in space.
Space Telescope Science Institute

It's a technique known as "transit spectroscopy," when light from a star travels through the atmosphere of an orbiting planet and reaches our telescopes – in space or on the ground – and tells about where it's been.

The Hubble Space Telescope has detected helium and water vapor in exoplanet atmospheres using spectroscopy; more detailed profiles of exoplanet atmospheres are coming from the James Webb Space Telescope , launched in 2021

Artist's concept of WASP-107b, a gas giant, orbiting a highly active K-type star about 200 light-years from Earth. Using spectroscopy, scientists detected helium escaping from the planet — the first time this element was found in an exoplanet atmosphere.

ESA/Hubble, NASA, M. Kornmesser

Another planet-hunting method takes advantage of an effect first described by Einstein: gravity's ability to warp and bend starlight. The gravity of a star in the foreground will magnify the light from a background star that passes just behind it. If the foreground star has a planet in orbit, the star will appear to a properly positioned telescope as a spike in light intensity as the background star goes by; the planet will appear as a second, smaller spike. NASA’s future Nancy Grace Roman Space Telescope will employ this technique, currently used by ground telescopes, to discover exoplanets.

The single pixels of light captured directly from exoplanets won't be enough to reveal surface features. But they will provide the next best thing: profiles of exoplanet atmospheres, and perhaps evidence of gases suggesting the presence of life.

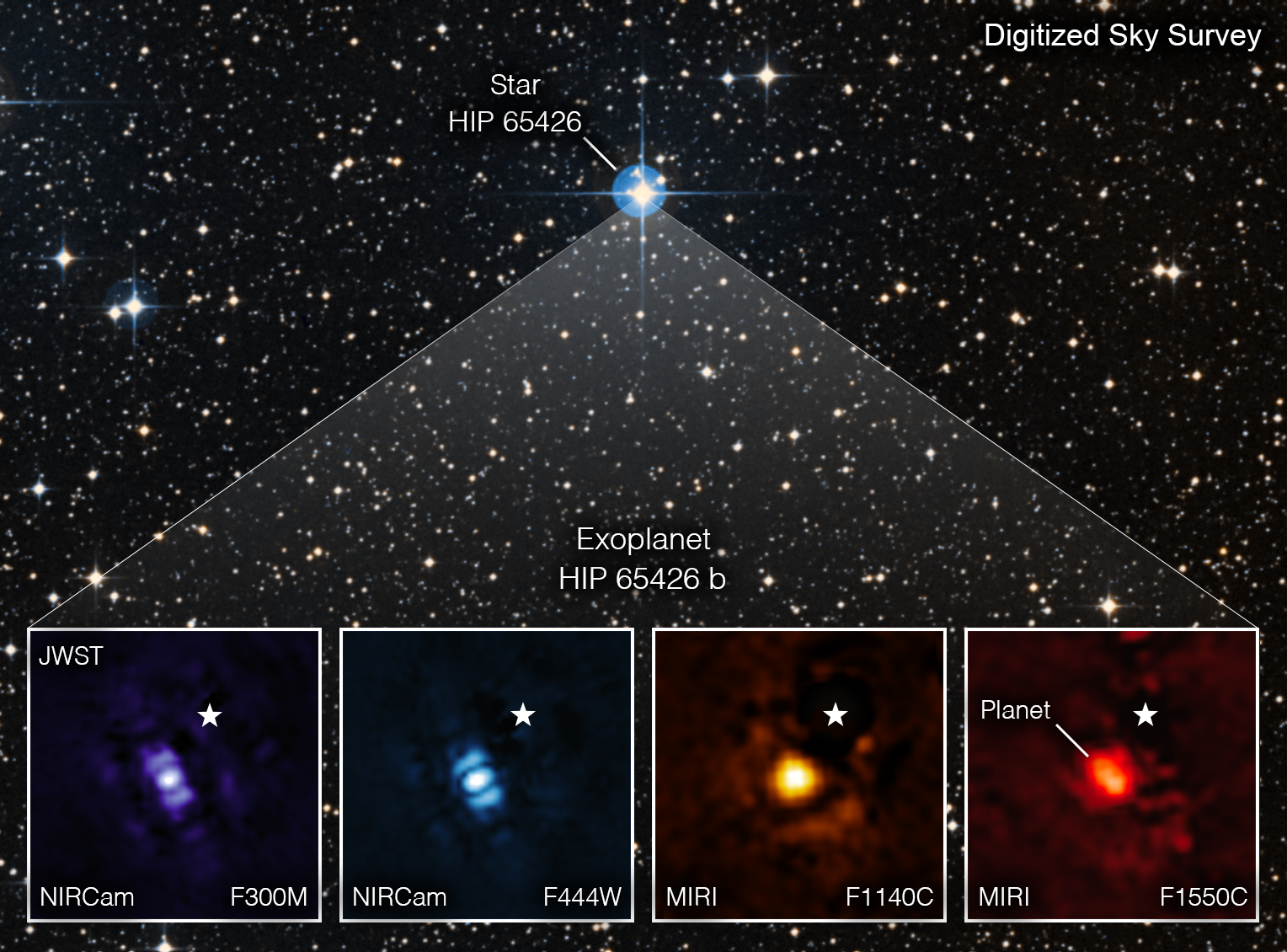
The star HIP 65425 & 4 views of its planet “b.” The background of the image is black with many white & blue stars; it is not from Webb and is labeled the “Digitized Sky Survey.” Star HIP 65425 is labeled at top center. It has 4 diffraction spikes (telescope artifacts) from the top, bottom, left, & right. Diagonal lines down from the star to the bottom of the image highlight 4 inset boxes. From left to right, first is Webb’s NIRCam view of the exoplanet. It's a purple dot with purple bars at 11 & 5 o’clock. The bars are telescope artifacts, not physically present. The planet & artifacts have been colored purple. The filter used, F300M (3 micrometers), is on the image. Next is a similar NIRCam view using filter F444W (4.44 micrometers). This view is colored blue & has the artifact bars. Next is a MIRI view, colored orange. No bars are present. The filter is F1140C (11.40 micrometers). Finally, a MIRI view using filter F1550C (15.50 micrometers). It is a red large dot. A white star icon on all 4 images represents the parent star.

The first direct image of an exoplanet from the James Webb Space Telescope shows HIP 65426 b in different bands of infrared light, as seen from : purple shows the NIRCam instrument’s view at 3.00 micrometers, blue shows the NIRCam instrument’s view at 4.44 micrometers, yellow shows the MIRI instrument’s view at 11.4 micrometers, and red shows the MIRI instrument’s view at 15.5 micrometers. These images look different because of the ways the different Webb instruments capture light. A set of masks within each instrument, called a coronagraph, blocks out the host star’s light so that the planet can be seen. The small white star in each image marks the location of the host star HIP 65426, which has been subtracted using the coronagraphs and image processing. The bar shapes in the NIRCam images are artifacts of the telescope’s optics, not objects in the scene.

NASA/ESA/CSA, A Carter (UCSC), the ERS 1386 team, and A. Pagan (STScI)

So far, such "direct images" of exoplanets have been mainly confined to giant planets still so hot from their fresh creation that they remain self-luminous.

One of the most striking is a movie of four exoplanets in orbit around the star HR 8799, created by astronomers using images from Hawaii's Keck Observatory.

A movie of four exoplanets in orbit around the star HR 8799, composed of seven years worth of images from the W.M. Keck Observatory in Hawaii.

Jason Wang and Christian Marois

The next generation of space telescopes would seek direct images of exoplanets using technology that is now under development: the coronagraph. The Nancy Grace Roman Space Telescope, set to launch in 2027, will test a coronagraph in space as a technology demonstration.

The coronagraph is meant to dim the overwhelming glare of stars to reveal the planets in orbit around them. And it all takes place inside the telescope: a system of masks, prisms and detectors that combine to suppress the starlight. It includes self-flexing mirrors, with thousands of tiny, piston-like actuators that flex in real time as the telescope captures light that has traveled tens of light years from an exoplanet. These "deformable mirrors" compensate for subtle flaws in telescope optics to squelch starlight and make the planet's light clearer.

When NASA's Nancy Grace Roman Space Telescope opens its eyes in the mid 2020s, it will peer at the universe through some of the most sophisticated sunglasses ever designed. This multi-layered technology, the coronagraph instrument, might more rightly be called "starglasses": a system of masks, prisms, detectors and even self-flexing mirrors built to block out the glare from distant stars — and reveal the planets in orbit around them.
NASA's Goddard Space Flight Center

Another starlight-snuffing technology is called the starshade. This sunflower-shaped spacecraft, the size of a baseball diamond, would unfold like origami. Parked far from a space telescope, its distinctive shape would block starlight and tamp down any stray light that might otherwise leak around the edges.

NASA scientists are working to refine the starshade design so it could be considered for a possible future mission.

This artist's concept of a starshade shows how the technology can block starlight and reveal the presence of planets. The video also shows the unfurling of a starshade model built by NASA's Jet Propulsion Laboratory, in an Astro Aerospace/Northroup Grumman facility in Santa Barbara in 2013.
NASA/JPL-Caltech

Next: NASA missions, aka The Planet Hunters

Keep Exploring